作者:Hans Knutson
来源:https://hackernoon.com/what-is-the-math-behind-elliptic-curve-cryptography-f61b25253da3
引言
某人要给你发送比特币时,他们是把比特币发送到你的地址上。要是你想花费你的地址上的这些比特币,你需要创建一笔交易来指定把比特币发送到哪里。一笔交易的含义就像下文:
从 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa(你的地址)转移 5 BTC 到 12c6DSiU4Rq3P4ZxziKxzrL5LmMBrzjrJX(收款人地址)
当然,任何人都能创建出上面这样的交易,所以,如果区块链会径直接受这种形式的交易,那无论是谁发起了它,你地址里面的 5 个比特币就会不翼而飞。幸运的是,区块链不会接受这种形式的交易,因为它缺少一个有效的数字签名(digital signature)。数字签名是用来证明你知道这个地址 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfN 对应的私钥的,如果你不知道对应的私钥,那 —— 你就不应该让人把钱发到这个地址,因为你没法花费其中的比特币!
你在给自己创建一个比特币地址(或者创建任意某种密码学货币的 地址/账户 时),你要先生成一个私钥。使用私钥,你可以计算出相应的公钥,并通过公钥哈希和转码生成相应的地址。幸好你不能先选择地址然后反向算出它的私钥,不然你就可以用同样的方法解出任何地址的私钥了。那还有 “账户” 这回事吗?
公钥密码学
公钥、私钥和数字签名,都是来自公钥密码学的基本概念。不论使用什么数学原理来实现一种公钥密码系统,它都必须满足下列属性(至少就我们的使用目的而言):
- 从给定的公钥倒推出相应的私钥在计算上是不可行的。
- 无需揭晓关于私钥的信息,就能证明一个人知道对应于某个公钥的私钥。进一步地,这样的证明可以被构造成需要结合一条具体的消息来验证。如此一来,这个证据就成了那条消息的数字签名。
打造公钥密码学的其中一种方法就是椭圆曲线。另一种办法是 RSA,它是围绕质数的。大部分的密码学货币 —— 包括比特币和以太坊 —— 都使用椭圆曲线,因为一个 256 位的椭圆曲线私钥跟一个 3072 位的 RSA 私钥的安全性相当。体积更小的私钥更易于管理和使用。
椭圆曲线密码学
那什么是椭圆曲线呢?一条椭圆曲线由满足下列形式的等式的所有点构成:
$$
y^2 = x^3 + ax + b
$$
同时 $4a^3 + 27b^2 \neq 0$ (这是为了避免奇点(singular points))。
下面是一些椭圆曲线的例子:
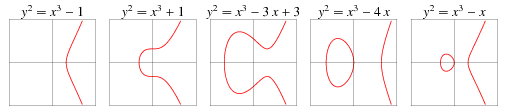
注意,上面所有的椭圆曲线都是 X 轴对称的。实际上,所有的椭圆曲线都如此,这是其形式所决定的。
$$
y^2 = x^3 + ax + b
$$
如果你取等式两边的平方根,就可以得到:
$$
y = \pm \sqrt{x^3 + ax + b}
$$
所以,如果取 a 为 27 而 b 为 2, 那么插入 x = 2 时,可得 y = ±8,也就是两个点 (2, -8)和(2, 8)。
下面这个椭圆曲线是比特币、以太坊等项目使用的椭圆曲线,叫做 “secp256k1”。这条曲线的等式是 $y^2 = x^3 + 7$,图像是:
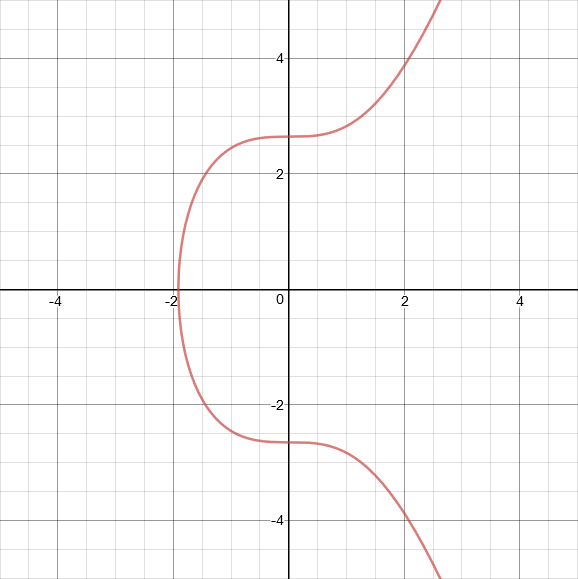
中本聪选择 spec256k1 并无特殊的理由。
点加法
你肯定知道如何把两个数相加,得出第三个数吧?在椭圆曲线上,你可以把两个点相加,得出第三个点。
要在一条椭圆曲线上把两个点相加,你先要找出一条穿过这两个点的直线。然后,这条直线与椭圆曲线的交点就是第三个点,最后,这个点跟 x 轴的对称点(也即其 y 坐标值乘以 -1 )即是两个点相加的结果。
我们来举个例子,假设我们要把下图所示的两个点相加:
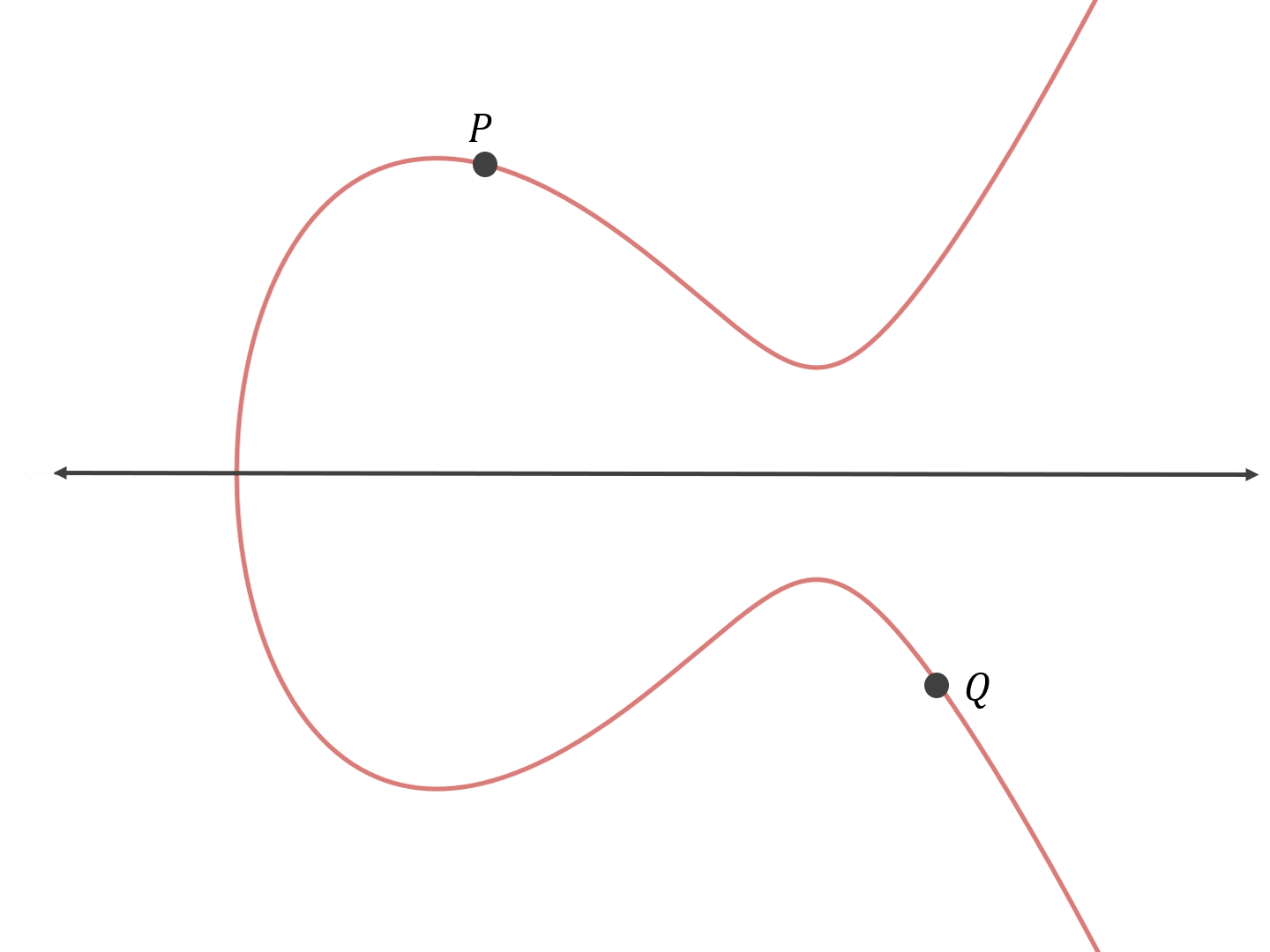
首先,作出一条穿过这两个点的直线:
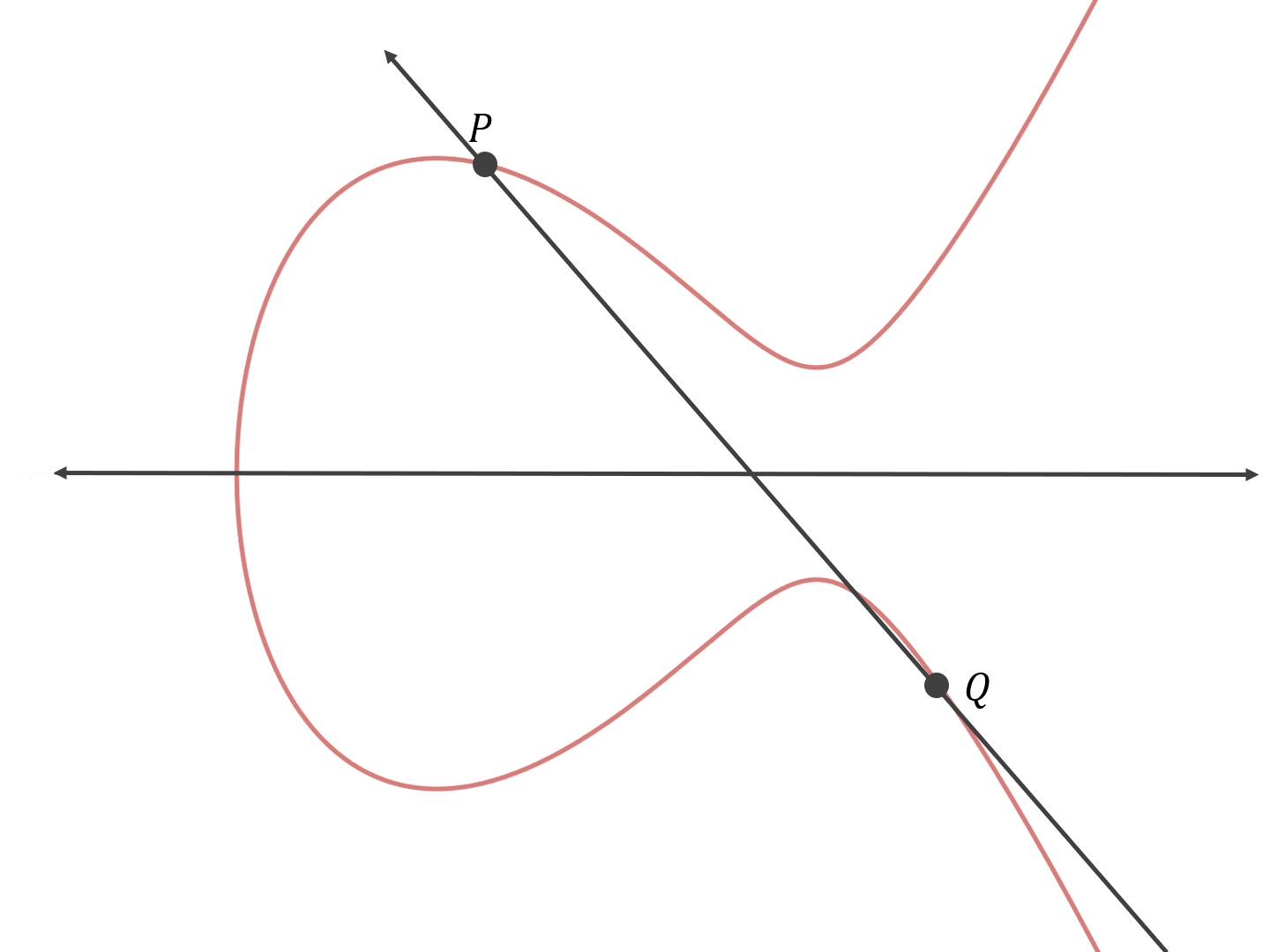
然后找出这条直线与椭圆曲线相交的点(第三个点):
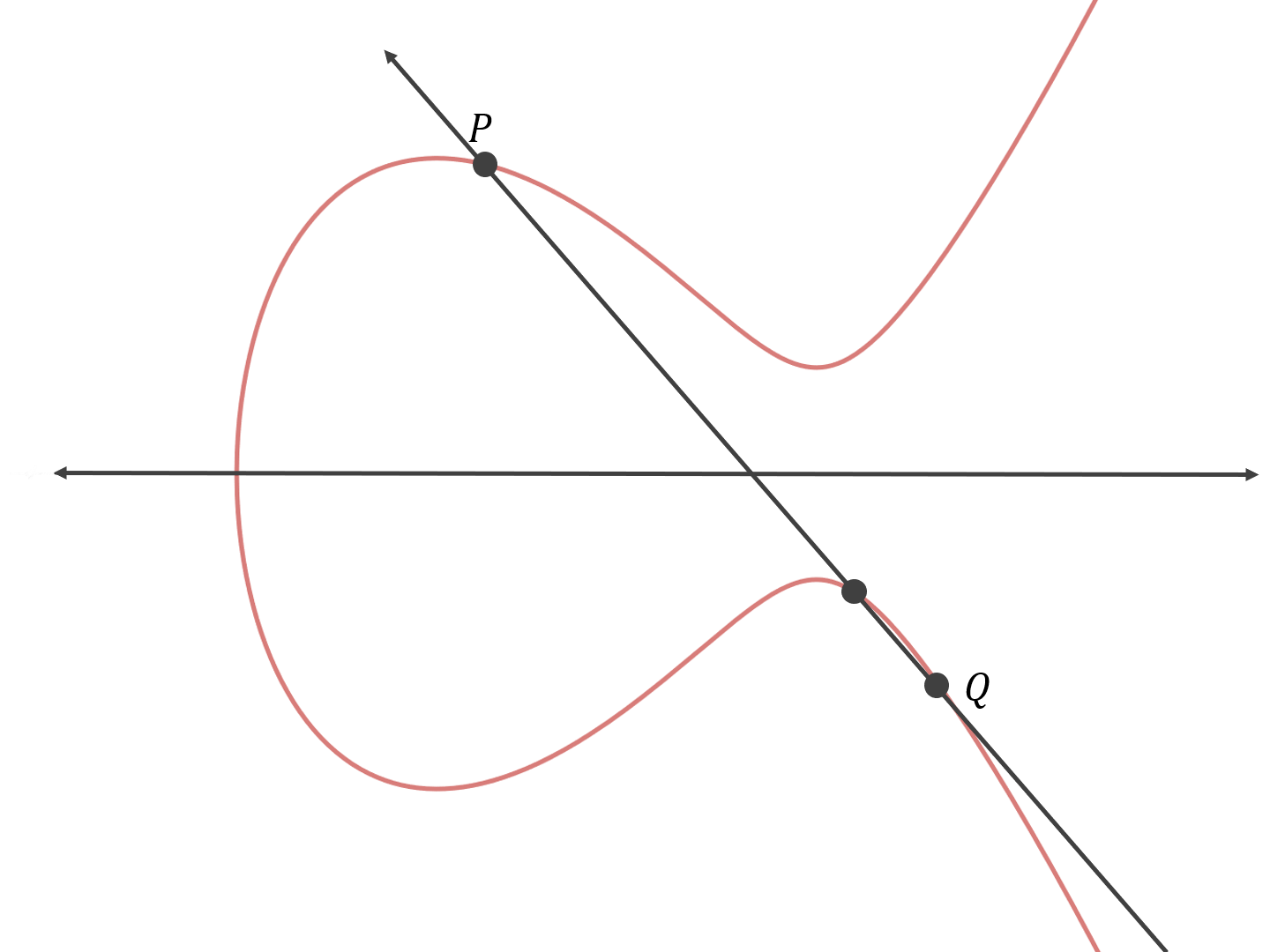
最后,找出与该点 x 轴对称的点:
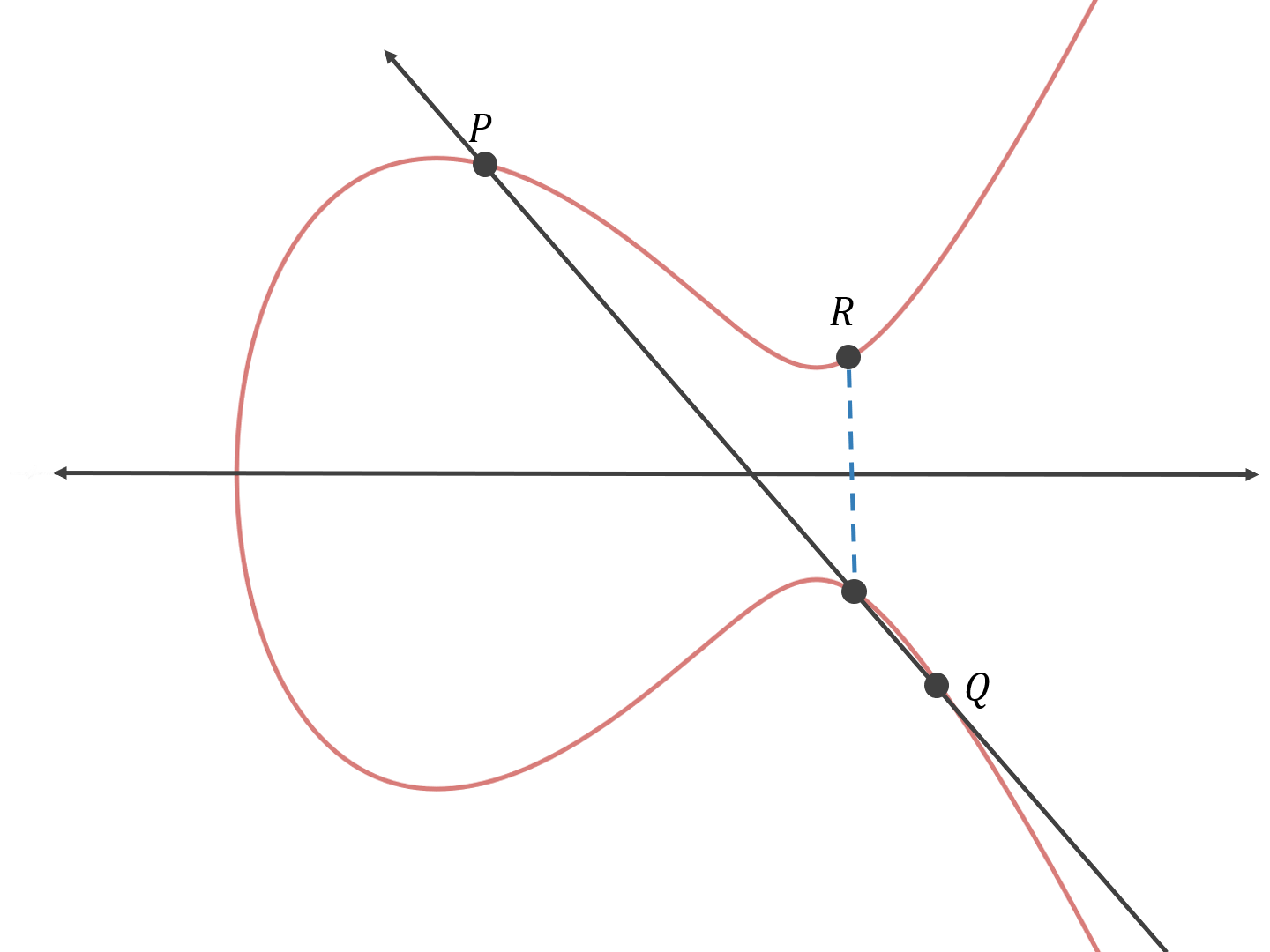
所以,P + Q = R。
为了方便实现椭圆曲线密码学,我们不是把两个点相加,而是在曲线上定义一个基本点,总是让这个点与自身相加。
举个例子,假设我们在下列曲线上有基本点 P:
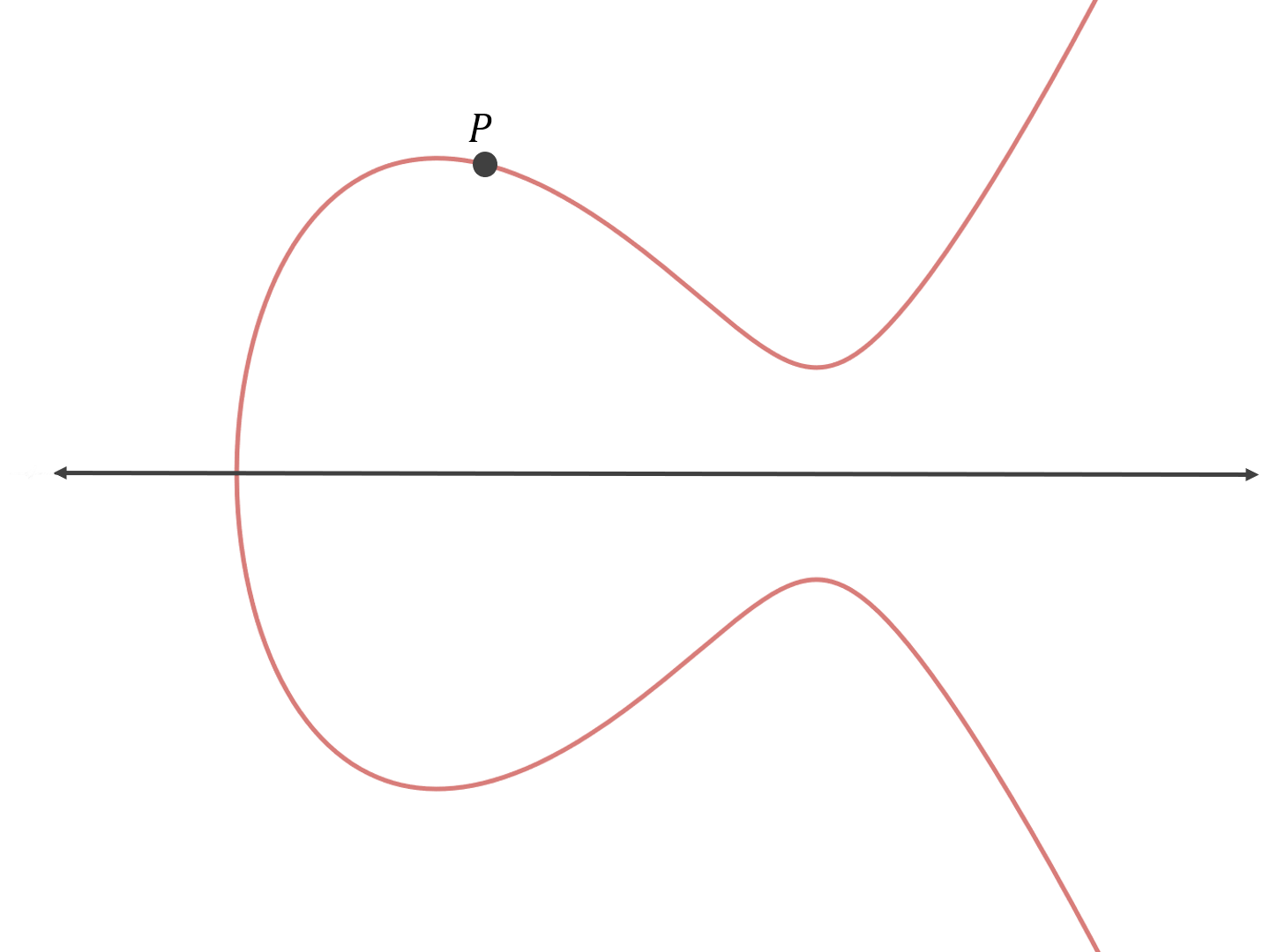
自然,我们就有了 P,或者说 1·P。
现在,我们让 P 与自身相加。首先,我们找出一个过 P 和 P 的直线(及其等式)。这样的直线有无数条!所以,在这种特殊的情形中,我们选择 P 点上椭圆曲线的切线:
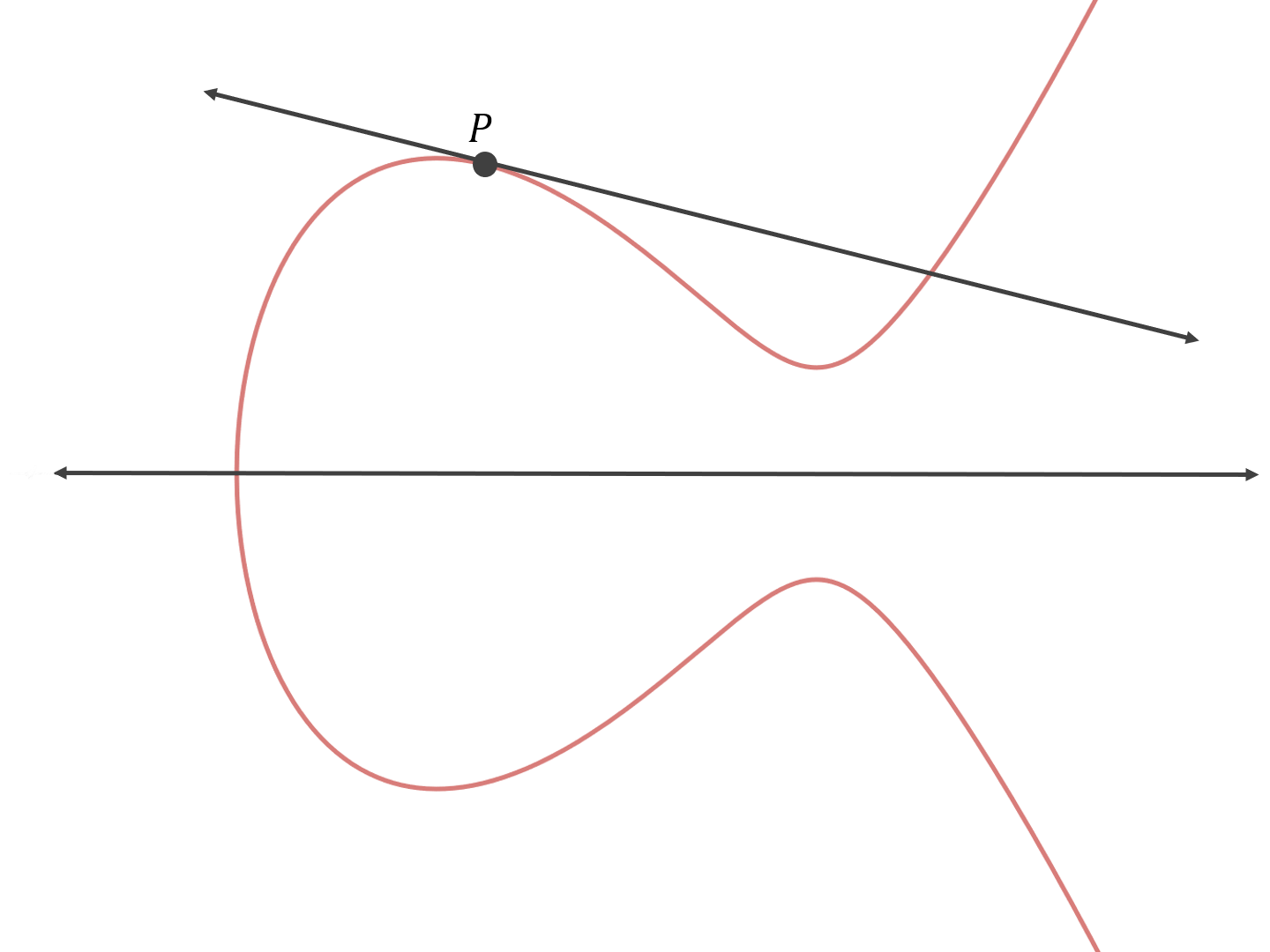
现在,我们可以找出 “第三点” 并通过 x 轴对称找到结果:
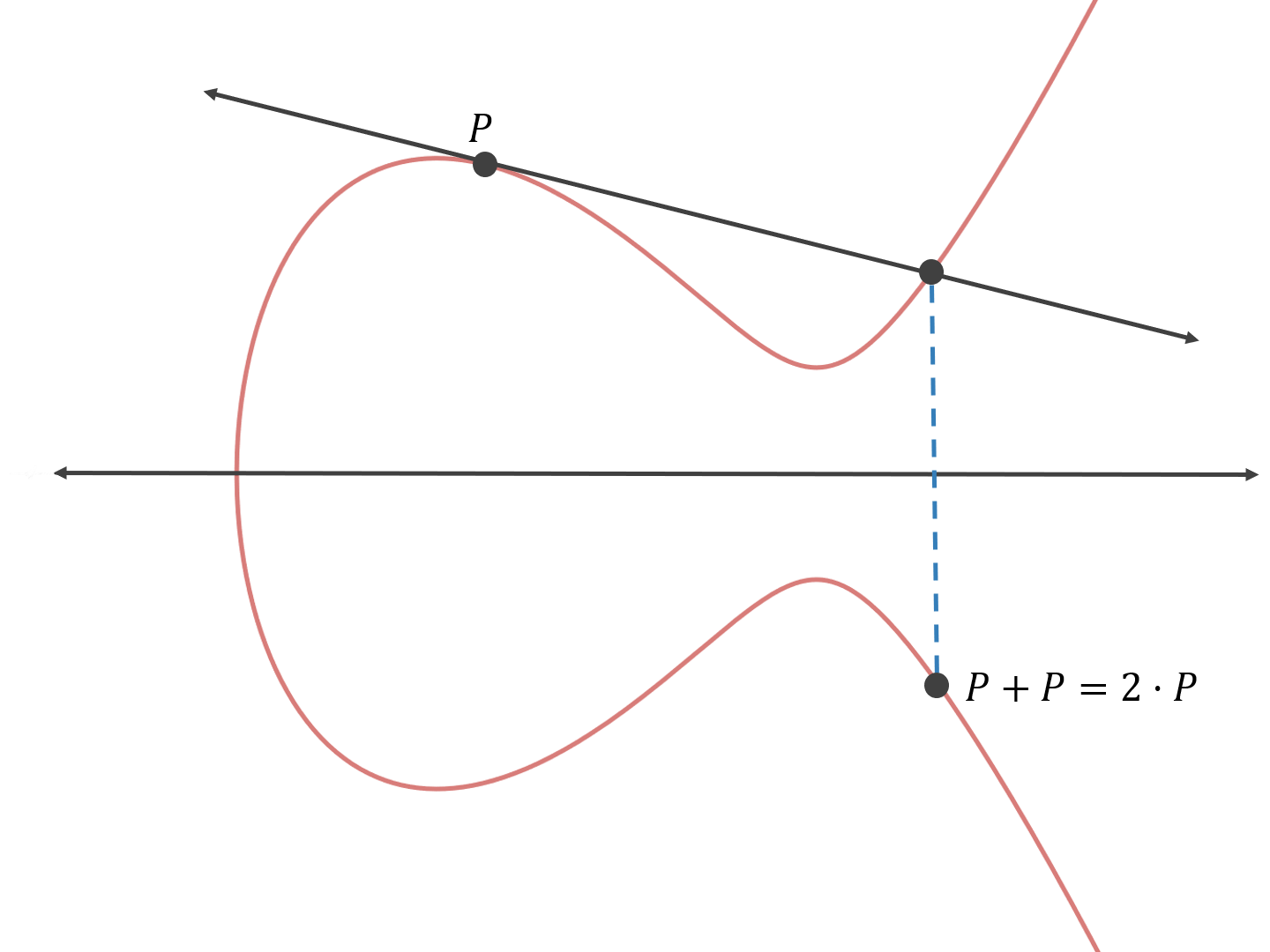
这就是 P 与自身相加的结果,P + P 或者说 2·P。
如果我们使之再与 P 相加,那是让 P 加上自身再加上自身,结果就是 3·P。为了计算 3·P,我们直接让两点相加即可:
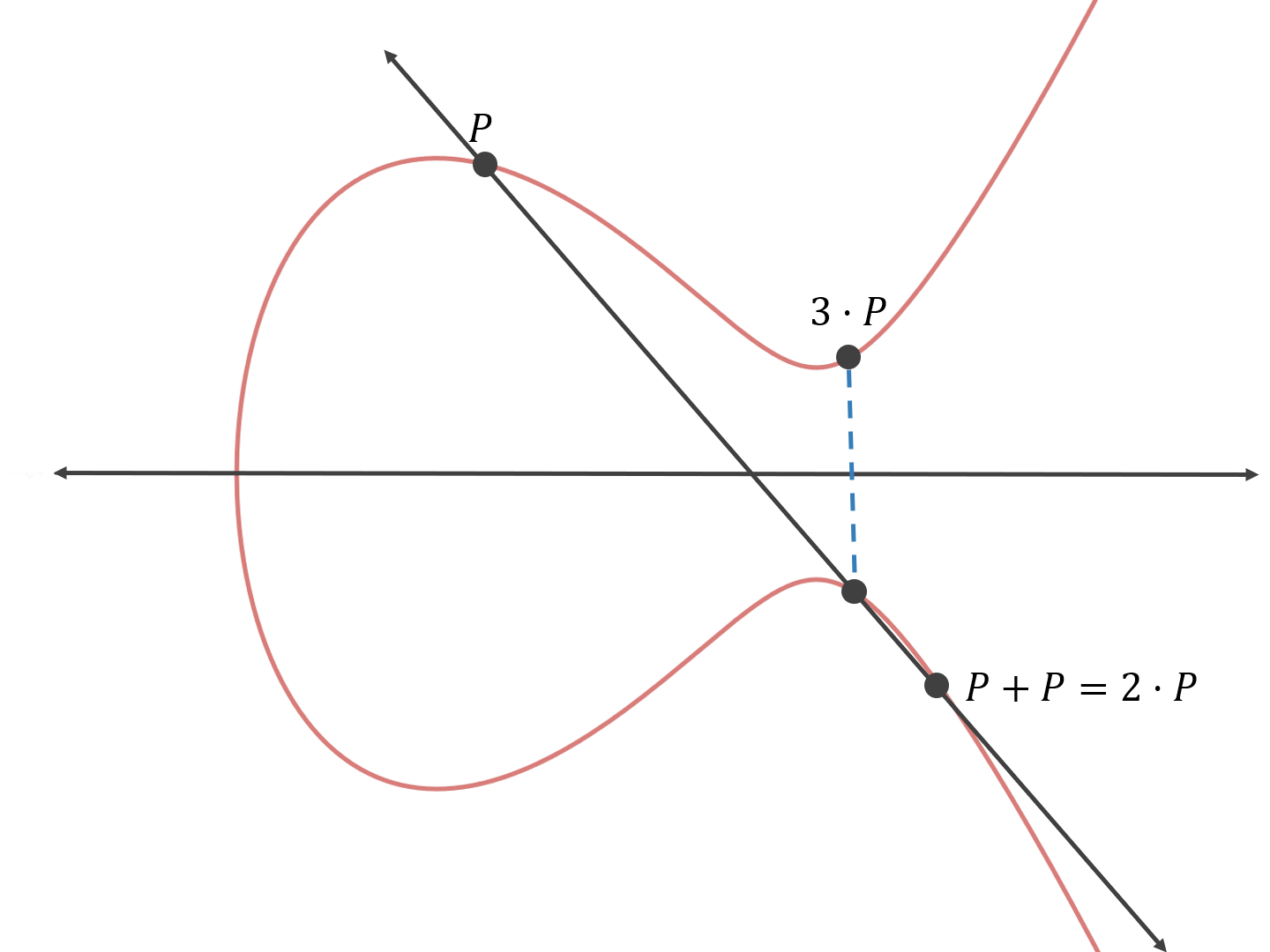
我们可以继续加下去,得出 4·P、5·P,等等。
secp256k1 所用的基本点的 x 坐标值和 y 坐标值为:
x 坐标值:55066263022277343669578718895168534326250603453777594175500187360389116729240
y 坐标值:32670510020758816978083085130507043184471273380659243275938904335757337482424
在上面的例子中,我们为了让所有的点都能在一个小窗口中显示,所以使用了不同的基本点。
快速点加法
如果你要计算 10·P,需要多少步呢?直觉来看,需要 9 步,因为 10·P 等于:
P + P + P + P + P + P + P + P + P + P
需要 9 次点加法。
但事实证明,你只需 4 步就可以计算 10·P,因为点加法满足下列属性:
n•P + r•P = (n + r)•P
举个例子:
4•P + 6•P = (4 + 6)•P = 10•P
那么,你可以这样计算 10·P:
P + P = 2•P
2•P + 2•P = 4•P
4•P + 4•P = 8•P
2•P + 8•P=10•P
这就只需要 4 次点加法。
那么,计算 x·P 需要多少步呢?x 是一个随机的 256 位整数,在我们这个例子中,x 的取值范围是从 0 到 1.1579209e+77。
事实又证明,你计算 x·P 最多只需要 510 次的点加法运算。解释一下:首先,你计算下列值:
2⁰•P、2¹•P、2²•P、2³•P、2⁴•P、2⁵•P、2⁶•P、…、2²⁵⁵•P
你可以用 255 次点加法计算出上面的所有值,因为这里有 256 个点,而你只要将前一个点与自身相加就可以得到后一个点。这是因为 $2^n•P + 2^n•P = 2^{n+1}•P$。
下一步就是找出 x 的二进制表示。举个例子,如果 x 是 246,那么其二进制展开就是 2⁷ + 2⁶ + 2⁵ + 2⁴ +2² + 2¹ = 246 。那么,我们就可以使用其二进制展开式来计算 246·P 的结果:2⁷•P + 2⁶•P + 2⁵•P + 2⁴•P + 2²•P + 2¹•P。我们不再需要一个一个点计算,因为这些点我们都提前算好了。
因为 x 的二进制展开式最多包含 256 个元素(从 2⁰ 到 2²⁵⁵),所以我们最多只需要把 256 个点相加,因此,最多只需要 255 次点加法。因此,总的来说,计算 x·P 最多只需要 510 次点加法。
椭圆曲线密码学中的私钥和公钥
假设我们要计算 x·P,而 x 是一个 256 位的随机整数。结果将是椭圆曲线上的一个点,我们称为点 X。
如果我给你 X,你能计算出 x 来吗?换句话来说,你能确定我相加了几次 P 来得到 X 吗?假设你是知道 P,也知道我使用的是哪条曲线。
事实证明,即使你拥有一台超级计算机,计算出 x 也是不可行的。没有已知的算法能计算出 x,所以你的唯一解法便是不断把 P 与自身相加,直至获得 X,或者从 X 中持续减去 P,直到结果就是 P。 x 是 0 到 2²⁵⁶-1 之间的某个数,所以其平均值为 2¹²⁸;因此,你需要做平均 2¹²⁸ 次点加法来求得 x。即使你的计算机可以每秒做 10000 亿次点加法,你从宇宙初创的那一刻开始跑计算机,到今天你也只能完成 2⁹⁸ 次点加法。而 2⁹⁸/2¹²⁸ =1/1073741824。
从正中间开始会不会快一点呢?比如,不到 510 步就能先算出 2¹²⁸•P。嗯,因为平均而言,x 接近 2¹²⁸ 的概率并不比它接近 0 或者 2²⁵⁶-1 的概率更大,它是随机分布的,所以你从哪里开始,结果都是一样的。平均而言你还是必须做 2¹²⁸ 次点加法。
私钥和公钥
所以,因为别人无法根据给定的 X 求得 x(X = x·P),所以 x 很适合用作你的私钥,而 X 就是你的公钥。因此,你的私钥是一个 256 位的随机整数,而公钥则是椭圆曲线上的点的 x 坐标值和 y 坐标值。这就满足了私钥和公钥所需的属性:
“从给定的公钥中推导出对应的私钥在计算上是不可行的”。
此外,虽然我们还没解释过,但确实,你可以无需揭示任何关于 x 的有用信息,就向别人证明你知道 x。也就是说,你可以向别人证明,你知道 P 与自身相加多少次可以得到 X,而无需告诉他们 x 到底是多少。
更新的椭圆曲线模型
在我们向其他人证明自己知道 x 之前,我们需要更新我们的椭圆曲线模型。
我们当前的模型的一个问题在于,x·P 的结果的 x 坐标值和 y 坐标值可能过大,无法存储在一个标准的 512 位的公钥中。x 坐标值和 y 坐标值都有可能过大。
接近方案是将我们的椭圆曲线定义在一个有限域上。基本上,就是确保只有椭圆曲线上只有整数点,而且这个点的坐标值是有上限的。
为达成这个目标,我们将等式
$$
y^2 = x^3 + ax + b
$$
转化成:
公式
y2 mod p = (x3 + ax + b) mod p
p 是某个指数(p 必须是质数,以保证加法和乘法总是能被还原(can always be undone))。
在 secp256k1 中, p 是小于 2²⁵⁶ 的最大质数。
我们的椭圆曲线因此看起来就像这样:
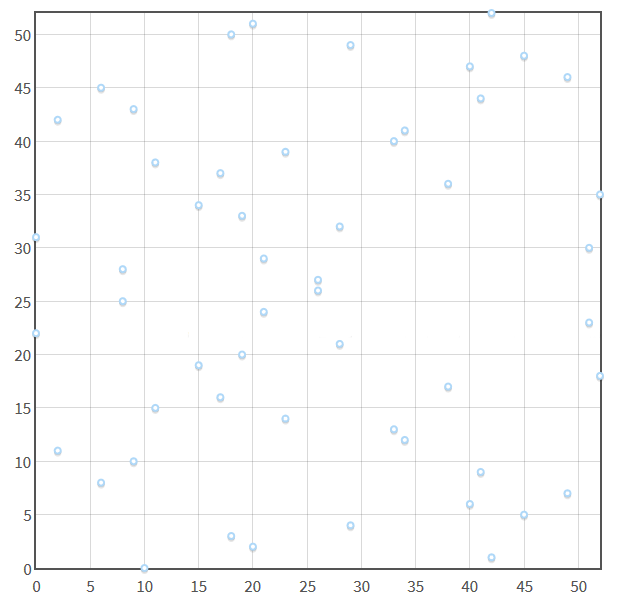
注意,这里依然有一条水平的对称线。
那么,现在你想把两个点相加,穿过这两个点的直线在跟第三个点相交之前就会飞到值域之外,那怎么办呢?让线从另一边开始继续延伸!
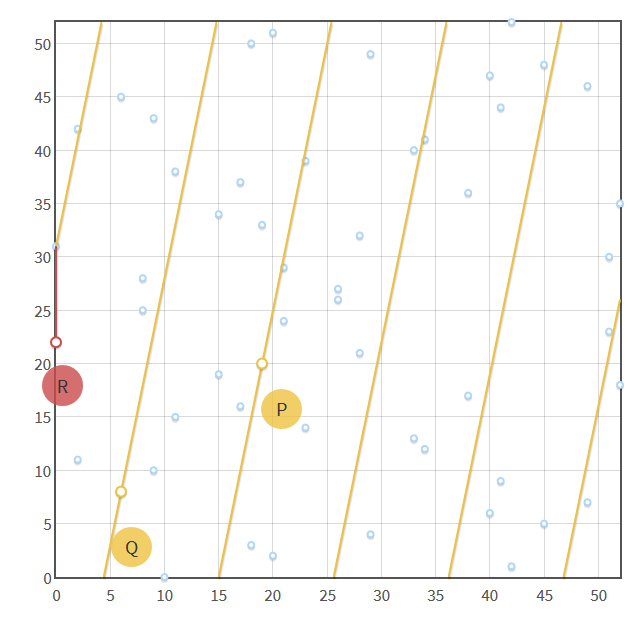
如上图所示,你会发现,把 P 跟 Q 相加需要让 P 跟 Q 之间的线来回环绕多次。
除了这个变化,其余东西都暂时不需要改变。
如何证明你知道 x
现在,你算出了 X = x·P,而 x 是一个 256 位的整数,你如何证明你知道对应于 X 的 x,且无需暴露关于 x 的任何有用信息呢?
你可以使用我们前面提到的点加法的属性:
n•P + r•P = (n + r)•P
稍微修改一下,可得:
hash(m, r•P)•n•P + r•P = (hash(m, r•P)*n + r)•P
你把方程的右半部分展开,就可以得到左边的部分,所以它对任意的 m、r 和 n,都是成立的。
那,不如我们令 n·P = X?这样就有:
hash(m, r•P)•X + r•P = (hash(m, r•P)*n + r)•P
如果 n·P = X,那 n 就等于 x,再转写一下,就是:
hash(m, r•P)•X + r•P = (hash(m, r•P)*x + r)•P
最后,我们做一下代换,令 R = r·P、 s = hash(m, R) * x + r 。
于是:
hash(m, R)•X + R = s•P
那么,我们再来回顾这个命题:如果你能提供一组 m、R 和 s,满足上述方程,那就能证明你知道对应于 X 的 x,即 x·P = X 。
要使该命题为真,需要满足两个前提:
- 只要你知道 x,那你就能提供合适的 m、R 和 s 值来满足上述方程
- 如果你不知道 x,那么你不可能找出满足上述方程的 m、R 和 s
如果你知道 x,显然你可以找出可以满足上述方程的值。选择随机的 m 和 r,然后计算 R = r·P,然后 s = hash(m, R) * x + r,代入方程 hash(m, R)•X + R = s•P,可得:
hash(m, r•P)•n•P + r•P = (hash(m, r•P)*n + r)•P
正是我们前面说的,对任意 m、r 和 n(在我们这里就是 x)都成立的等式。
那要是你不知道 x 呢?你可以计算出能满足上述方程的 m、R 和 s 吗?问题就在于,你要解出 hash(m,R)•X + R = s•P。基本上,你这是要找出一个哈希值的原像,而这是不可能的,至少在计算上是不可行的,因为密码学哈希函数有原像攻击抗性。
因此,唯一能够提供有效的 m、R 和 s 值的方法就是使用 x 来计算它们。因此,你可以通过提供满足等式 hash(m, R)•X + R = s•P 的 m、R 和 s 值来证明你知道 x。
在这个过程中,你真的没有暴露关于 x 的信息吗?
如果你已经提供了有效的 m、R 和 s,别人能从中知道关于 x 的有效信息吗?
m 和 R 都跟 x 无关,所以这些值不会暴露关于 x 的有效信息。
而我们知道,s = hash(m, R) * x + r 。能不能从 s 中计算出 x 呢?
这就是在讨论,我们能否解出 x = (s-r)/hash(m, R) 。
因为我们不知道 r,所以无法从 s 中计算出 x。而我们也无法从 R = r·P 中计算出 r,因为这就是想知道 P 与自己相加多少次能得到 R,也就是想从 X 中知道 x,在计算上是不可能的。
s 也不会暴露关于 x 的信息(比如 “x 必然小于 bala bala”)。如果 r 是随机生成的,而我们允许 hash(m, R) * x + r 溢出使得 r 可以是任何 256 位的整数,那么 s 的值就是完全随机的,s 可以是任何 256 位的整数。一个随机的 256 位整数,所蕴含的有关 x 的信息,恐怕就跟新西兰的 GDP 所蕴含的一样多。
数字签名
m、R 和 s 可以用来证明某人知道相应于 X 的 x(X = x·P)。验证这个证据需要把 m、R 和 s 代入等式 hash(m,R)•X + R = s•P。那么,我们是否能然验证依赖于一条特定的消息,使得这个证据 —— m、R 和 s —— 变成对该消息的一个数字签名?当然可以!
假设 m 就是那条消息,而 R 和 s 就是这条消息的数字签名。验证将仅在这条消息,也即是 m,代入验证等式之时,才会成功。如果代入的是另一条消息,则左右两边将不相等,因为计算 s 所用的 m 值与代入得消息不等。
因此,你可以通过提供一个数字签名 R 和 s,以及相应的消息 m,来证明你知道相应于公钥 X 的私钥 x。
在密码学货币中,这个消息就是一笔交易的待签名的部分。一条交易的数字签名,通常是 R 的 x 坐标值后面跟着 s(R 是椭圆曲线上的一个点,s 是近乎随机的 256 位整数),然后还要编码成十六进制的形式。
(译者注:作者在此处解释的数字签名方案,并不是比特币和以太坊一开始使用的 ECDSA 签名,而是一种叫做 “Schnorr 签名” 的方案(的简化版)。在 2021 年 12 月以前,比特币上也无法使用 Schnorr 签名,而只能使用 ECDSA 签名;2021 年 12 月,比特币激活 taproot 升级,该升级便引入了 Schnorr 签名,从此比特币交易可以使用 Schnorr 签名方案了。)
结论
如果你想获得一个比特币地址或者以太坊账户,你只需生成一个随机的 256 位整数 x,x 就是你的私钥。然后你使用 secp256k1 的参数就可以计算出公钥 X = x·P。你的公钥可以放心地展示给别人,无法用来反算出你的私钥。再对公钥哈希计算,就得到了地址。
(译者注:以太坊的地址确实是这样得出来地,但是比特币的地址需要经过更多的编码步骤,不过原理上是差不多的)。
当你想把自己地址里的比特币发给其他人时,你要创建一笔比特币交易。把交易的待签名部分设置成 m,并使用该 m 计算出 R 和 s。然后在交易中附加上 R 和 s。在你把这笔交易广播到比特币网络中以后,收到交易的节点会验证 m(交易的待签名部分)、R 和 s 满足等式 hash(m,R)•X + R = s•P。当然,这也假设了你要在交易中提供 X,因为你的公钥无法从地址中推测出来。在以太坊交易中,你无需提供 X,可以提供 v,v 可用来从 R 和 s 中计算出 X。
(译者注:再次提醒,作者解释的并不是 ECDSA 签名算法,而是 Schnorr 签名算法,该算法在 2021 年 12 月之后才能在比特币上使用。)
(完)