作者:benma & Sebastian
来源:https://blog.bitbox.swiss/en/understanding-silent-payments-part-one/

我们骄傲地宣布, BitBox02 是第一款能够安全地执行比特币 “静默支付” 的硬件签名器。在这个系列博客中,我们希望展示静默支付的工作原理,以及在表象之下,BitBox02 做了什么,来让这些支付能够安全地执行。
发送到静默支付地址的支持将在未来的更新中提供给所有 BitBox02 用户。
- 第一篇将解释静默支付的工作原理
- 第二篇将展示为安全地支持静默支付,BitBox02 在背后都做了什么
静默支付是一个提议新的比特币地址格式的 BIP(比特币优化提议)。它的主要好处是能产生一种静态的地址。它消除了管理多个地址的需要,同时还能保护隐私性。如果你想了解更多基础概念,可以看看我们上一篇关于可复用支付码的文章。
当前,为了保护隐私,链上支付的收款方必须在每一次收取支付时,给支付方提供一个新的地址。者导致了糟糕的用户体验,以及使用困难。
举个例子:
- 从交易所取款:在每一次取款的时候,你都要从 BitBoxApp 中找出一个新的、还没用过的地址,在 BitBox 和第二台设备中验证这是正确的地址,最后到交易所登记这个地址。
- 向交易所存款:每一次存款,你都要在交易所创建一个新的存款地址,并在发送资金之前在第二台设备和 BitBox 上验证它是一个有效地址。
- 接收捐款:你需要建立和运营一个服务器(比如 BTCPay Server),以为每一次捐赠生成一个新的地址。
许多比特币服务端和用户都不想处理这样的复杂性,所以他们直接重复使用同一个地址,这就牺牲了他们的隐私性,因为他们所有的交易都会关联到同一个地址,很容易被识别和分析。
静默支付的目标是解决上述挑战。其地址的设计目标是可以复用(静态),但发送到静默支付地址的交易将只有发送者和接收者(地址的主人)才能识别出来。所以慈善机构可以在网页中公开一个稳定不变的捐款地址,而不让任何人知道谁捐了钱、捐了多少。交易所也可以为你所有的取款登记一个静默支付地址。
比特币交易
比特币的交易由输入和输出组成。

输出会产生新的 UTXO(未花费的交易输出),而输入则是花费现有的 UTXO 。如果关于 “UTXO” 你想了解更多,可以看看我们关于这个主题的文章。
最常见的情况是,一个 UTXO 是用一个公钥来锁定的,而要花费它的时候,需要提供一个由该公钥背后的私钥所生成的签名。当你为比特币交易填入一个地址的时候,通常,这个地址就编码了一个公钥(或者一个公钥的哈希值)。
静默支付使用了一些有趣的密码学技术,为发送给一个静默支付地址的每一笔交易都派生一个新的、没有用过的公钥。现在,让我们来了解一下这背后的知识和直觉。下文是对静默支付工作原理的简化的、概要的描述。想要了解所有的细节,还是得看它的 BIP 本身。
迷你入门课:私钥和公钥
私钥就是一个很大的数字,长到无法猜测出来,比如说:
$92193805913277071008055984303319191614197341949664602874511898854633635443214$
每一个私钥都能生成一个对应的公钥。公钥不会暴露其背后的私钥的任何信息。
从技术上来说,公钥属于一个数学上特殊的 “群”,它有自己专门的假发。如果你想了解更多,《 椭圆曲线密码学:通俗介绍 》这个系列博客是非常好的材料。
从私钥生成公钥的公式是:
$公钥 = 私钥 \times G$
这里的 $G$ 是预定义的值,称为 “生成元”。生成元是一个特殊的公钥。所有其它的公钥,都是通过生成元和加法,生成出来的。
比如说,如果你的私钥是 $2$ ,那么,你的公钥就是 $2 \times G = G + G$ 。如果你的私钥是 $3$ ,那你的公钥就是 $3 \times G = G + G + G$ ,依此类推。 当然,在实际用途中,你的私钥会是一个非常大的、怎么猜也猜不到的数字,就像上面那个例子。
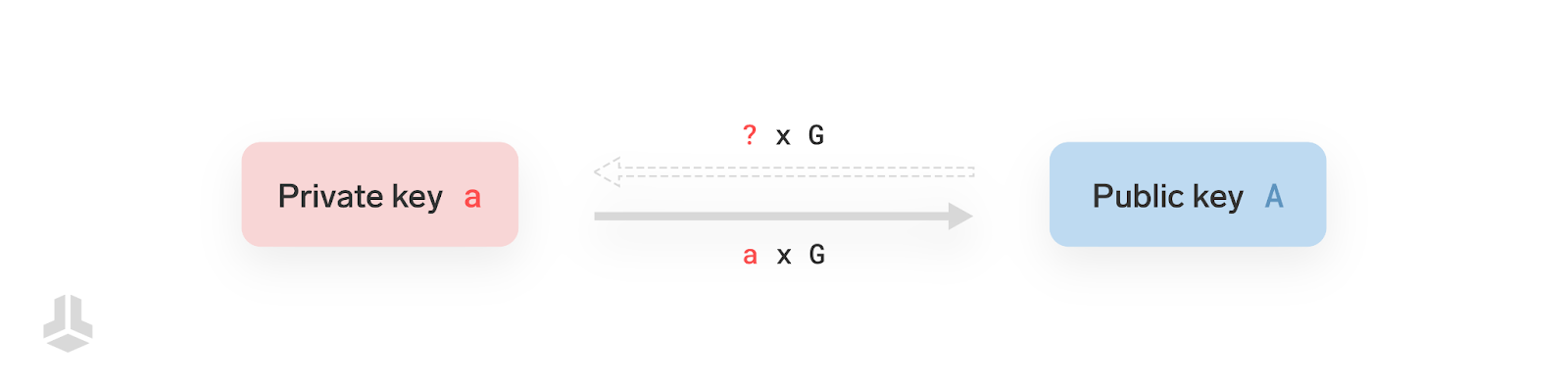
除了不能反向计算,大部分常用的数学,在公钥所在的群里也是一样的。比如大家熟悉的 “结合律”,依然成立:
$(a + b) \times G = a \times G + b \times G$
在本文剩余的章节中,我们用小写字母来表示私钥,用大写字母来表示公钥。例如:$a \times G = A$ 。
椭圆曲线上的 Diffie-Hellman 密钥交换
“椭圆曲线上的 Diffie-Hellman 密钥交换(ECDH)” 是一套简单的协议,为两个参与者 Alice 和 Bob 创建一个他们共享的秘密值。
我们假设 Alice 要给 Bob 发送一笔交易。
- Alice 的公私钥对:$a \times G = A$
- Bob 的公私钥对:$b \times G = B$
只需要把自己的公钥交给对方,他们就可以创建一个只有他们俩知道的秘密值。
- Alice 计算共享秘密值: $S = a \times B$
- Bob 计算共享秘密值:$S = b \times A$
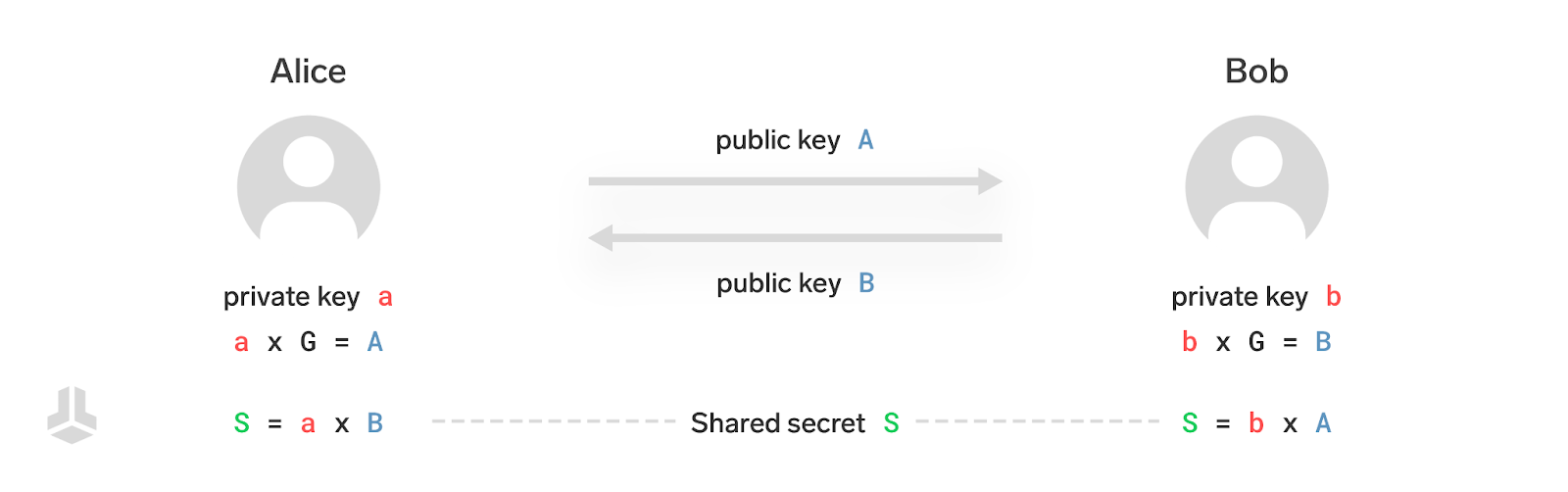
你可以看出,两个数值是一样的:
$$
S = a \times B = a \times (b \times G) = a \times b \times G = b \times a \times G = b \times (a \times G) = b \times A
$$
技术上来说,$S$ 是私钥 $a \times b$ 所对应的公钥,可以用在交易的输出中,作为锁定输出的公钥,但是,需要让 Alice 和 Bob 的私钥结合起来,才能花费它。
为了避免分享私钥,我们可以通过哈希算法,将它转化为一个新的私钥:$s = hash(S)$ 。从而,我们可以用这样的公钥来锁定输出:
$$
P = hash(S) \times G = hash(a \times B) \times G = hash(b \times A) \times G
$$
被这个公钥锁定的资金,可以被发送者和接收者任何一方(使用自己的私钥)花费。那怎么做到让它只能被 Bob 花费呢?接着往下看。
静默支付
静默支付地址的前缀为 sp1(而不是我们熟悉的 bc1),而且,它看起来是这样的:
$$
sp1qqgste7k9hx0qftg6qmwlkqtwuy6cycyavzmzj85c6qdfhjdpdjtdgqjuexzk6murw56suy3e0rd2cgqvycxttddwsvgxe2usfpxumr70xc9pkqwv
$$
非常长对吧?因为它编码了接收者的两个公钥:一个用于扫描的公钥 $B_{scan}$,一个用于花费的公钥 $B_{spend}$ 。额外的公钥,是为了让只有 Bob 才能花费。
在发送交易的时候,Alice 为 Bob 安排的输出所用的公钥不是 $P = hash(S) \times G$,而是加入了 Bob 的第二个公钥的调整版本:$P = B_{spend} + hash(S) \times G$ 。至于 $S$ ,Alice 用 Bob 的扫描公钥和自己的私钥计算出来:$S = a \times B_{scan}$ 。
Alice 能计算出公钥 $P$,是因为她从 Bob 的静默支付地址中知道了 $B_{scan}$ 和 $B_{spend}$ ,而且她知道自己的私钥 $a$ 。
最终的公钥 $P$ 会用来锁定添加到交易的一个 Taproot 输出。
只有 Bob ,才能够用自己的两个私钥 $b_{spend}$ 和 $b_{scan}$ 来花费这个输出中的资金,因为只有他才知道 $P$ 背后的私钥:
$$
P = B_{spend} + hash(S) \times G = b_{spend} \times G + hash(b_{scan} \times A) \times G = (b_{spend} + hash(b_{scan} \times A)) \times G
$$
所以,Bob 最后用来花费这个输出的私钥就是:$p = b_{spend} + hash(b_{scan} \times A)$ 。
Bob 使用自己的扫描私钥计算出共享秘密值的哈希值 $hash(S) = hash(b_{scan} \times A)$ ,再加入自己的花费私钥,就可以计算出最终的私钥。
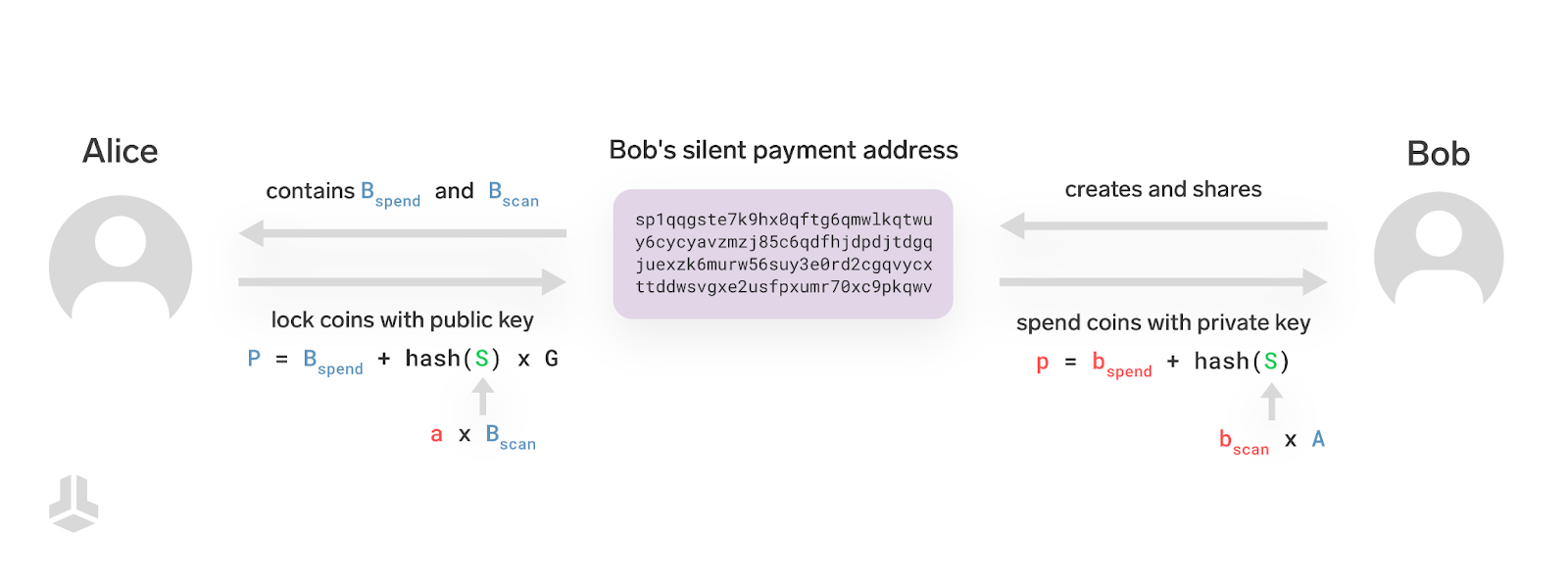
那么 Alice 到底使用哪个私钥呢?Bob 怎么知道这个私钥所对应的公钥?
Alice 想给 Bob 支付,她知道 Bob 的公钥,因为 Bob 所公开的静默支付地址里面有。
那么 Alice 的密钥呢?Bob 怎么知道 Alice 所用的公钥?不知道 Alice 的公钥,不就没办法重新创建出共享秘密值、也无法探测出发给他的静默支付交易、更没法花费资金了嘛?要是接收者还需要跟每个支付者沟通、获得对方的公钥,那就很不方便。
解决方案非常优雅:所有附加到交易本身的有关密钥!
Alice 花费自己的 UTXO、制作发送给 Bob 的交易;这些 UTXO 本身分别被一个 公私钥对 锁定。她需要自己的私钥来花费自己的资金,那何不直接使用这些私钥来创建共享秘密值呢?
所以,Alice 拿自己用作交易输入的所有 UTXO 的私钥,来创建用在静默支付中的共享秘密值。
Bob 可以通过所有交易输入的公钥,计算出共享秘密值。
一笔交易可能有多个输入,所以 Alice 要使用一个结合私钥,就是所有输入的私钥之和:
$a = a_1 + a_2 + …$
Bob 也要使用交易的结合公钥,也就是所有交易输入的公钥之和:
$A = A_1 + A_2 + …$
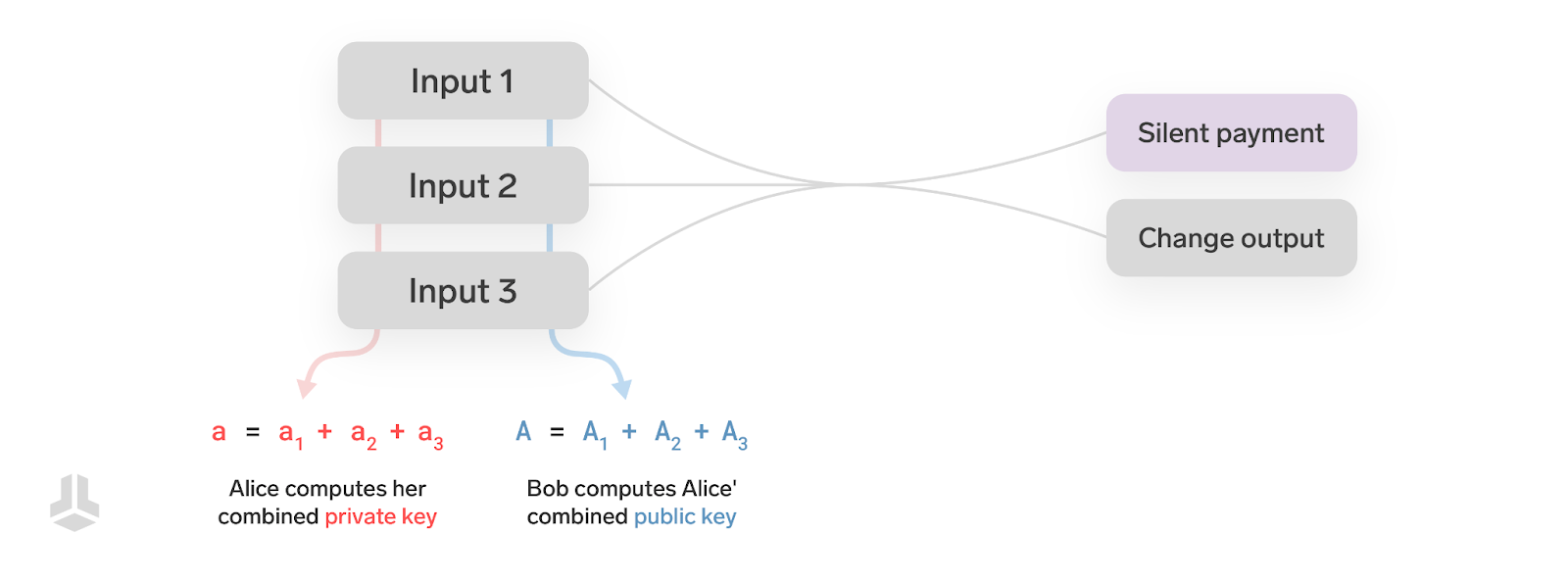
根据结合律,这些私钥的和正是公钥的和所对应的私钥:
$$
A = (a_1 + a_2 + …) \times G = a_1 \times G + a_2 \times G + … = A_1 + A_2 + …
$$
为了实现上述效果,每一个输入都必须有且仅有一个相关的公钥。因此,静默支付仅允许使用下列脚本类型的输入:P2TR(且要求是密钥花费)、P2WPKH、P2WPKH-P2SH、P2PKH;换句话说,之允许使用单签名的脚本类型,这也是当前最常见的类型。不幸的是,如果 Alice 用的是一个原生的多签名脚本(而不是 MuSig2 或其它能够聚合成单个公钥的聚合签名方案),或者是其它高级脚本,就无法发起静默支付。我认为这是静默支付的一个很大的缺点,也是阻止其得到采用的巨大障碍。
确保地址不会复用
静默支付的主要目标是避免 地址/公钥 复用。根据上述方案,接收者的公钥是从 Alice 在交易输入中的公钥和 Bob 的静默支付地址中动态创建出来的。然而,如果 Alice 一直使用同一个地址,那么她发送给 Bob 的静默支付地址的多笔交易,会因为使用相同的输入公钥而产生相同的输出公钥。
为了解决这个问题,静默支付提议规定,输出公钥并不像上文那样计算($P = B_{spend} + hash(S) \times G$);而要这么计算:
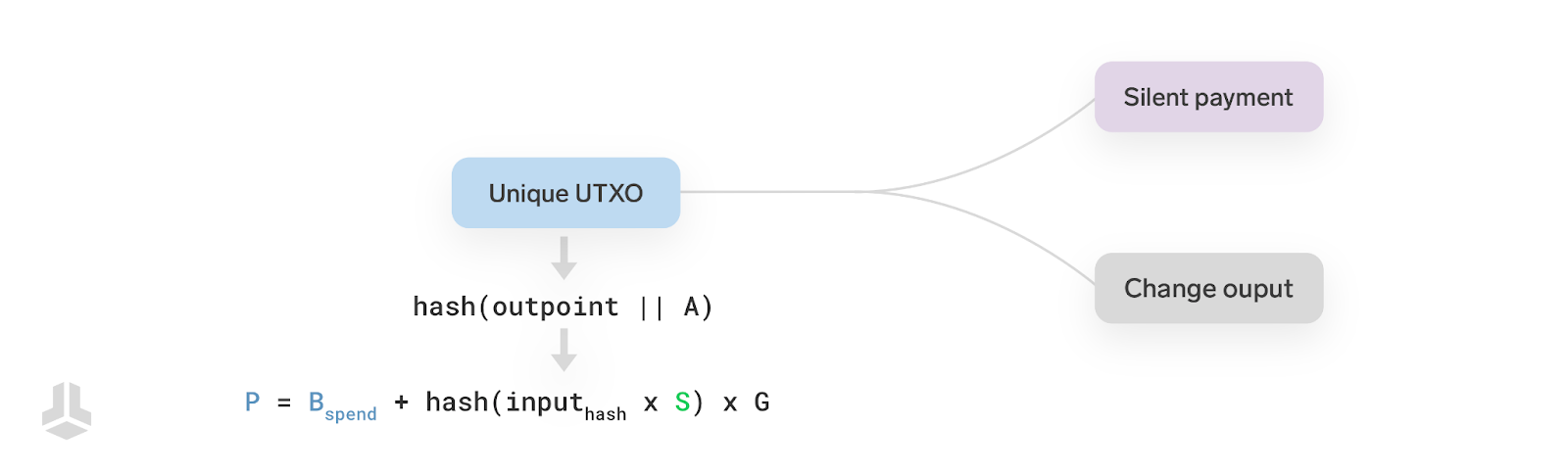
$P = B_{spend} + hash(input_{hash} \times S) \times G$
这里的 $input_{hash} = hash(outpoint || A)$ ,也就是交易的其中一个输入的输出点与公钥的字节拼接的哈希值。输入的 “输出点” 是一个交易 ID 和一个输出索引号,是 UTXO 的唯一标识符。因为 UTXO 在比特币区块链上无法重复花费,那么 UTXO 的唯一标识符的哈希值就保证了独一无二的输出公钥,因为没有两个 UTXO 会有同样的标识符。出于 BIP 所说的一个技术理由,$A$ 也放在哈希函数中。
在提议的最初草案中,input_hash 是根据所有交易输入(在运行字典排序后)计算出来的。在我的评审意见中,我指出这对硬件签名器是个挑战(点击页面中的 “Show resolved” 来展开帖子:
这对硬件签名器是个挑战。硬件签名器的内存有限,也许无法加载所有的输出点并加以排序。因此,将不得不限制交易为在签名时刻已经有排好序的输入,这是不理想的,而且会产生兼容性问题。
与其使用排好序的输出点的哈希值,也许我们可以使用 ……
在许多人参与讨论之后,能够满足要求、也适合硬件签名器的解决方案出现了:仅哈希一个输入,在字典排序中最小的哪个输入。这产生了该 BIP 的最终版本,并让 BitBox02 可以无摩擦地实现对静默支付的支持。
总结
我们介绍了静默支付的概念;作为一个比特币优化提议,它提出了一种新的地址格式,让用户可以重复使用一个静态地址,同时保护隐私性。我们介绍了私钥和公钥的基本概念,讨论了使用 ECDH 来创建共享秘密值的过,以及这种技术如何用来锁定资金、保证只有接收者才能花费它们。
在下一篇文章中,我们将了解静默支付如何改变了硬件签名器的角色,以及为了安全地支持静默支付 ,硬件签名器要做哪些事情。