作者:David Wong
来源:https://www.cryptologie.net/posts/hash-based-signatures-part-i-one-time-signatures-ots/
Lamport 签名
1979 年 10 月 18 日,Leslie Lamport 出版了他发明的一次性签名。
绝大部分签名方案的安全证明都部分依赖于单向函数(one-way functions),一般来说是哈希函数。而 Lamport 方案的优雅之处在于,这种签名仅仅依赖于这些这些单向函数的安全性。
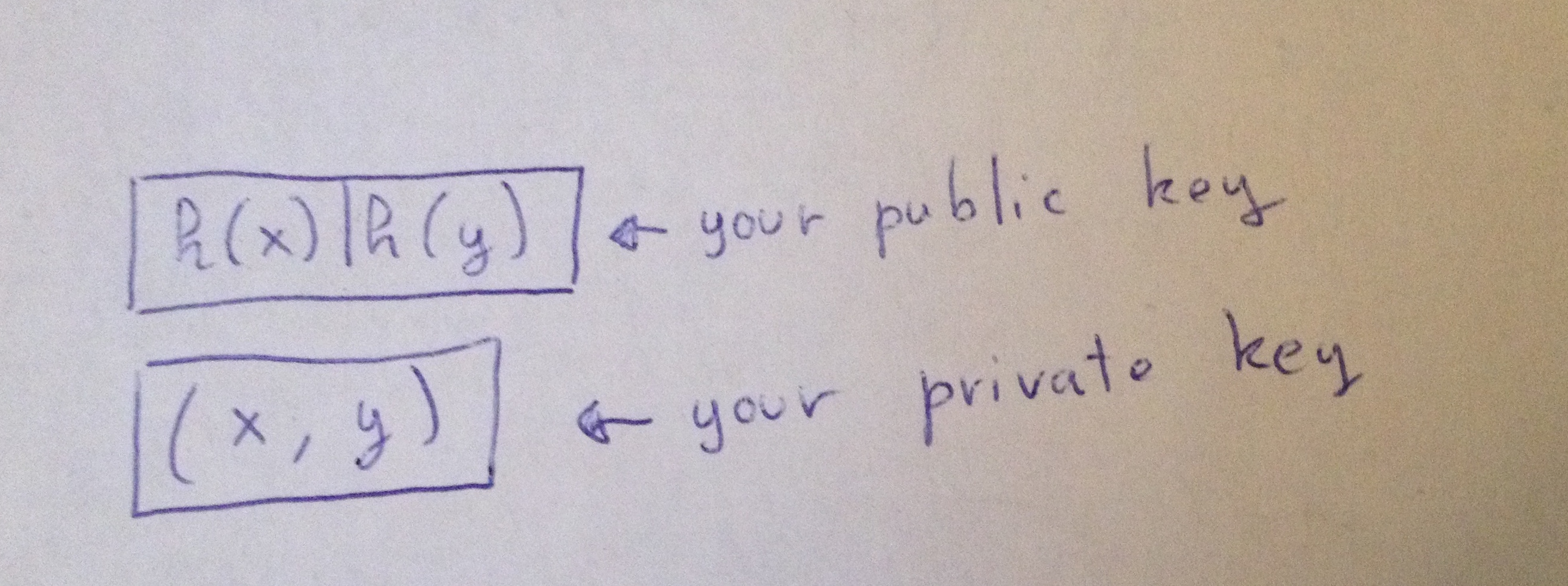
(H(x) | H(y)) <-- 你的公钥
(x, y) <-- 你的私钥
Lamport 是一种非常简单的方案,首先 x 和 y 都是整数,要签名一个比特的时候:
- 如果这个比特的值是
0,那就发布x - 如果这个比特的值是
1,那就发布y
非常简单对吧?但显然,你不能用同一个公钥重复签名。
那么,如果要签名多个比特的话,该怎么办呢?你可以先把自己要签名的消息哈希一下,比如放到 SHA-256 哈希函数里面(其输出的长度是可以预测的,从而,固定下要签名的东西的长度)。
现在,(要签名 256 个比特),你需要 256 个私钥对:

(H(x_0) | H(y_0) | H(x_1) | H(y_1) | ... | H(x_255) | H(y_255)) <-- 你的公钥
(x_0, y_0, x_1, y_1, ... x_255, y_255) <-- 你的私钥
举个例子,如果你要签名 100110,那么你需要发布 (y_0, x_1, x_2, y_3, y_4, x_5)。
Winternitz OTS(WOTS)
Lamport 的论文出版的几个月后,斯坦福大学数学系的 Robert Winternitz 提出,可以公开 $h^w(x)$ 而非 $h(x) | h(y)$

(译者注:以整数 x 作为一次性签名的私钥,用 H(x) 用来签名数字 1,用 H(H(x)) 来签名数字 2,以此类推;假设你要签名的最大数字为 n,则 x 连续哈希 n + 1 次的结果即是你的公钥。)
比如说,你可以选择 $w = 16$,并公开 $h^{16}(x)$ 作为公钥,仅仅需要保存 $x$ 作为你的私钥。现在,假设你要签名二进制的 $1010$,也就是十进制里的 $9$ ,只需要公开 $h^{9}(x)$ 即可。
现在,另一个问题在于,恶意人看到这个签名之后,就可以哈希它;比如说,再哈希一次,就可以得到 $h^{10}(x)$ ,也就是伪造你对二进制 1010(或十进制的 10)的有效签名。
Winternitz 一次性签名的变种
很久以后,在 2011 年 Buchmann 等人出版了对 Winternitz 一次性签名的更新,引入了一个变种:使用以一个密钥作为参数的函数的家族。你可以把它(这种函数)理解为一种 “消息认证码(MAC,message authentication codes)”。
现在,你的私钥变成了一组密钥,它们将用在 MAC 中,而消息将决定我们会将这个 MAC 迭代多少次。这是一种特殊的迭代,因为上一轮迭代的输出会替换掉用在函数中的密钥,并且我们给函数的输入总是相同的,也是公开的。来看一个例子吧:
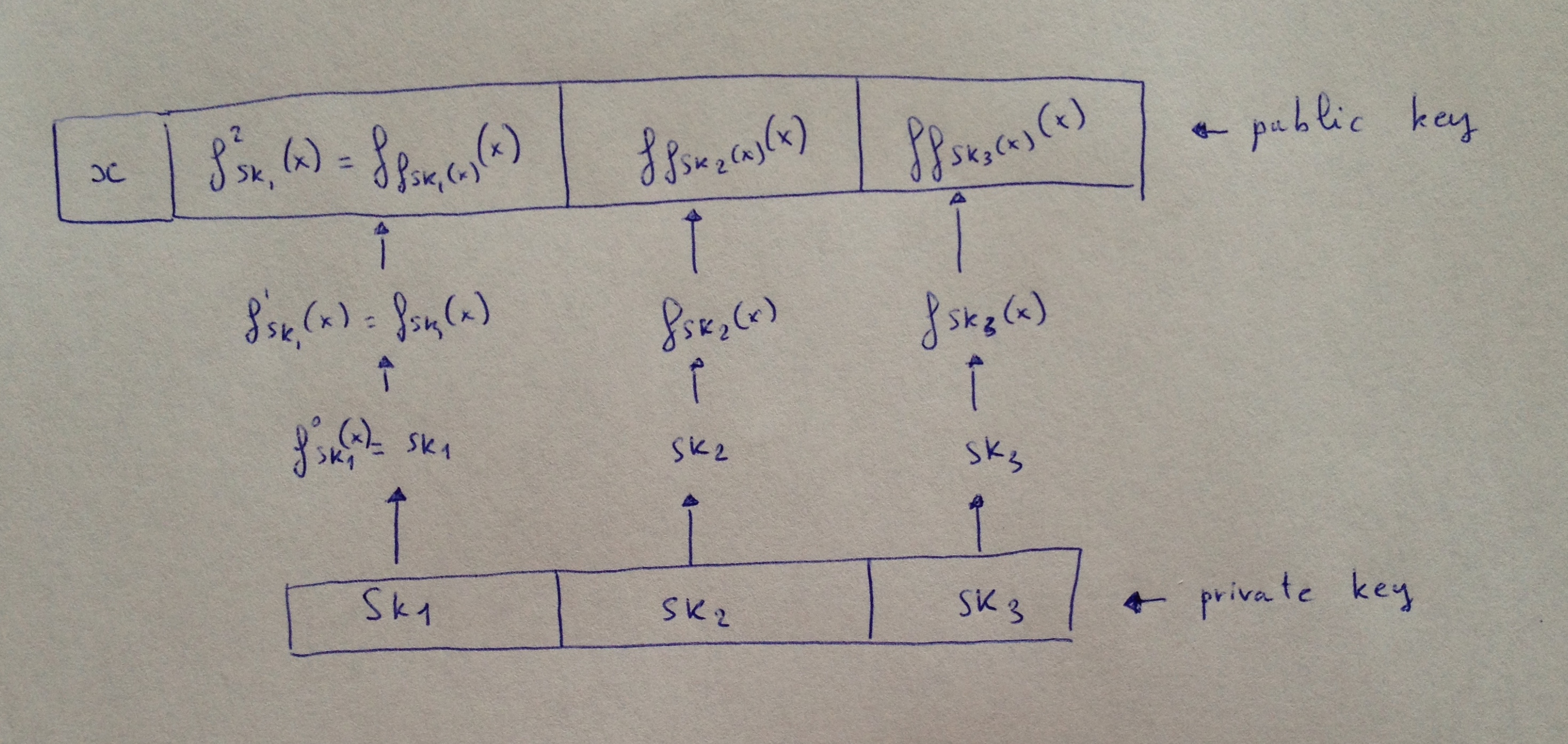
(译者注:如图,先生成一组密钥 sk_i。对数值 0 的签名就是 sk_i 本身。然后,为了签名数值 1 以及更大的数值,对任意一个 sk_i,以 sk_i 作为参数,以 x 为输入运行一次函数,即为一次迭代;迭代所得到的值,将成为下一轮迭代的参数。x 是公钥的一部分,始终是公开的。)
我们要签名的消息是二进制的 1011,也就是十进制的 11。假设我们的 W-OTS 变种在基数为 3 时可以工作(事实上,基数为任意的 w 时都可以工作)。所以,我们将消息转化为三进制下的 $M = (M_0, M_1, M_2) = (1, 0, 2)$ 。
要签名这条消息,我们只需公布 $(f_{sk_1}(x), sk_2, f^2_{sk_3}(x))$ 即可,其中最后一项 $f^2_{sk_3}(x) = f_{f_{sk_3}(x)}(x))$ 。
请注意,有个事我没在这里讲,但我们的消息是有个校验和(cheksum)的,这个校验和也需要签名。这就是为什么 $(M_2 = 2)$ 的签名在公钥中已经暴露也没有关系。
直觉告诉我们,增加一轮迭代的公钥可以提供更好的安全性。

以下是 Andres Hulsing 在他关于这个话题的演讲中提到我之后给出的回答:
为什么呢?以比特 1 为例:校验和将是 0 。因此,要签名这条消息,你只需要知道一个公钥元素的原像。为了让这个方案安全,它的难度必须与安全参数呈指数增长。要求一个攻击者可以在两个数值上逆转哈希函数,或者在同一个数值上逆转两次,只会让攻击复杂性乘以 2 。这并不会显著增加这个方案的安全性。从比特安全性的角度看,你可能只获得了多 1 比特的安全性(而代价是运行时间变成 2 倍)。
(译者注:“比特安全性” 衡量的是需要运行多少次暴力搜索来攻破一个方案。比如 “80 比特的安全性”,意味着你要运行 $2^{80}$ 次搜索。)
Winternitz OTS+(WOTS+)
关于 W-OTS+ 方案,就没有太多要说的了。上述变种出现的两年以后,Hulsing 独自出版了一项升级,可以缩短签名的体积并提高安全性。在以密钥为参数的函数家族之外,它还使用了一个连锁函数(chaining function)。在更新后的方案中,在每一轮迭代中,密钥总是相同的,只是输入变成了上一轮迭代的输出。并且,在对这个上一轮的输出应用单向函数之前,还要将它与一个随机的数值(或称 “掩码”)运行异或运算(XOR)。
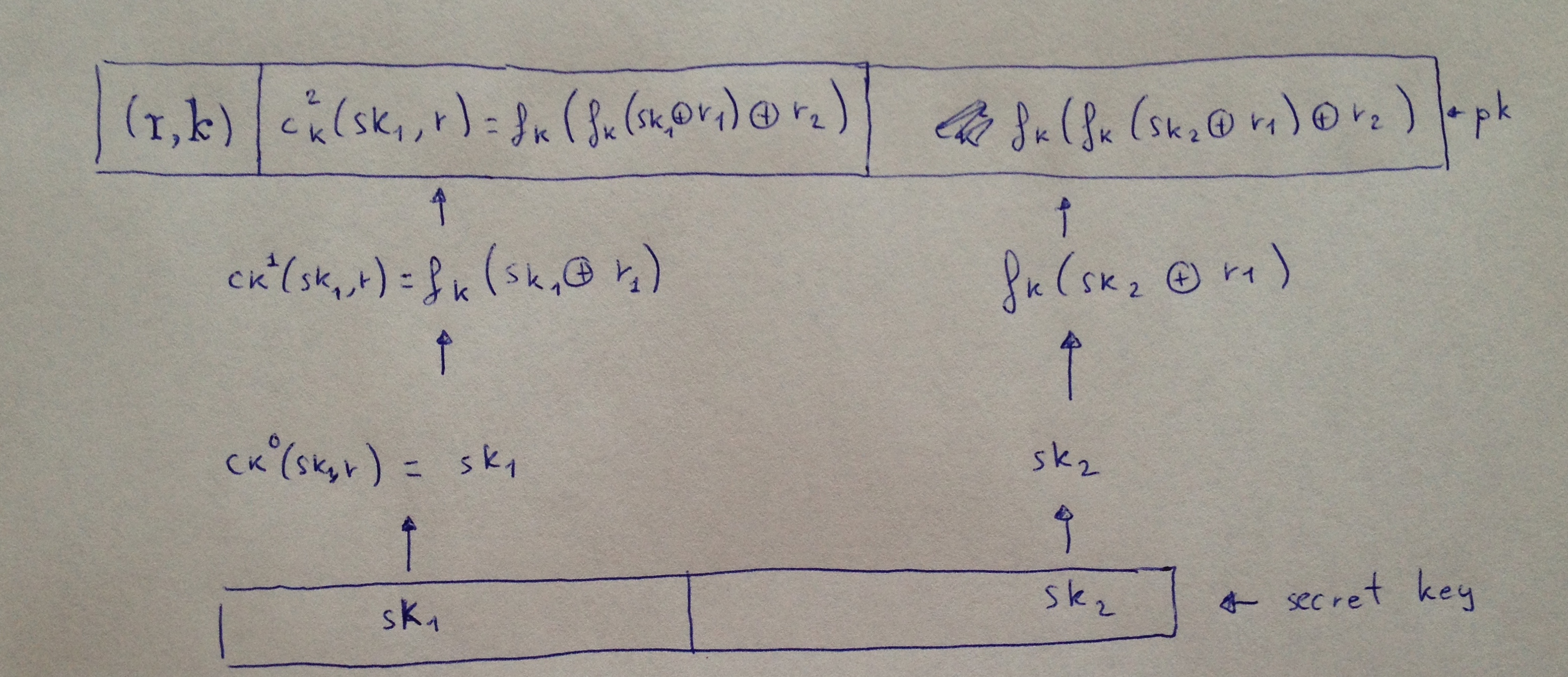
来自 Hulsing 关于缩短签名的精确描述:
WOTS+ 可以缩短签名的体积,是因为你可以使用输出更短的哈希函数(相比于相同安全量级或者更长哈希链条的其它 WOTS 变种。换句话说,如果为所有的 WOTS 变种使用相同的哈希函数、相同的输出长度和相同的 Winternitz 参数
w,WOTS+ 能实现比其它变种更高的安全性。这一点的重要性在于,举个例子,如果你想要使用一个 128 比特的哈希函数 —— 不要忘了,最初的 WOTS 要求哈希函数是抗碰撞的(collision resistant),但我们在 2011 年提出的变种以及 WOTS+ 相应只要求 伪随机函数/第二原像抗性哈希函数 —— 在这种情况下,原本 WOTS 只能实现 64 比特的安全性,可以说是不安全的。而我们 2011 年的提议和 WOTS+ 可以实现128 - f(m, w)比特的安全性。至于后两者的差别,WOTS-2011 的f(m, w)与w呈线性增长;而 WOTS+ 的f(m, w)与 w 呈对数增长。
其它 OTS
今天的博客到这里就结束了!但还有很多一次性签名方案,如果你有兴趣,这里有一个列表,其中有一些超越了一次性签名,因为它们可以少量复用。所以,我们可以称之为 “少量次数签名方案(FTS)”:
- 1994, The Bleichenbacher-Maurer OTS
- 2001, The BiBa OTS
- 2002, HORS
- 2014, HORST (HORS with Trees)
到目前为止,诉诸应用的似乎收缩到了基于哈希函数的签名,因为它们是当前为了后量子安全而建议使用的签名方案。详见几个月前发布的《后量子密码学初步建议》。
又:感谢 Andreas Hulsing 的评论