作者:David Wong
来源:https://cryptologie.net/posts/hash-based-signatures-part-iii-many-times-signatures/
在本系列前面的文章中,我们已经了一次性签名(OTS)以及少量次数签名(FTS)。现在,是时候看看如何基于哈希函数获得实用的签名方案了 —— 可以使用同一私钥多次签名的方案,最好是想签多少次就能签多少次。
如果你还没有读过本系列的第一篇和第二篇文章,也不全然是坏事,因为我们会作一些抽象。只需要把 OTS 当成一对你只能用一次(签名一条消息)的公私钥对就好。
Dumb trees
最早出现的想法是使用一堆的一次性签名(就使用你喜欢的 OTS 方案)。第一次要签名的时候,你就使用第一对 OTS 密钥,并且绝不重用;第二次要签名的时候,你就使用第二对 OTS 密钥,并且绝不重用。如是不断重复 —— 我很确定你知道我要说什么。这会非常糟糕,因为你的公钥将由所有的 OTS 公钥组成;如果你希望能够签名很多次,那就必须准备大量的 OTS 公钥。
减少需要存储的(私钥的)数量的一种办法是,使用一个种子,然后以伪随机数生成器来生成所有的私钥。这样一来,你就不需要存储任何私钥,只需存储种子就可以了。
但是,公钥的体积将依然很大,大到完全不实用。
默克尔树
要将所有这些 OTS 公钥连接起来、变成一个主公钥,有一种非常简单的方法,那就是使用默克尔树。这个解决方案是由拉尔夫·默克尔(Ralf Merkle)在 1979 年发明的,但由于一些并不有趣的编辑问题,直到 10 年之后才出版。
以下是一个非常简单的定义:默克尔树是一种基础的二叉树,其每一个节点都是其子节点的哈希值。我们将 OTS 公钥作为默克尔树的叶子,树根就是主公要。所谓一图胜千言,请看图:
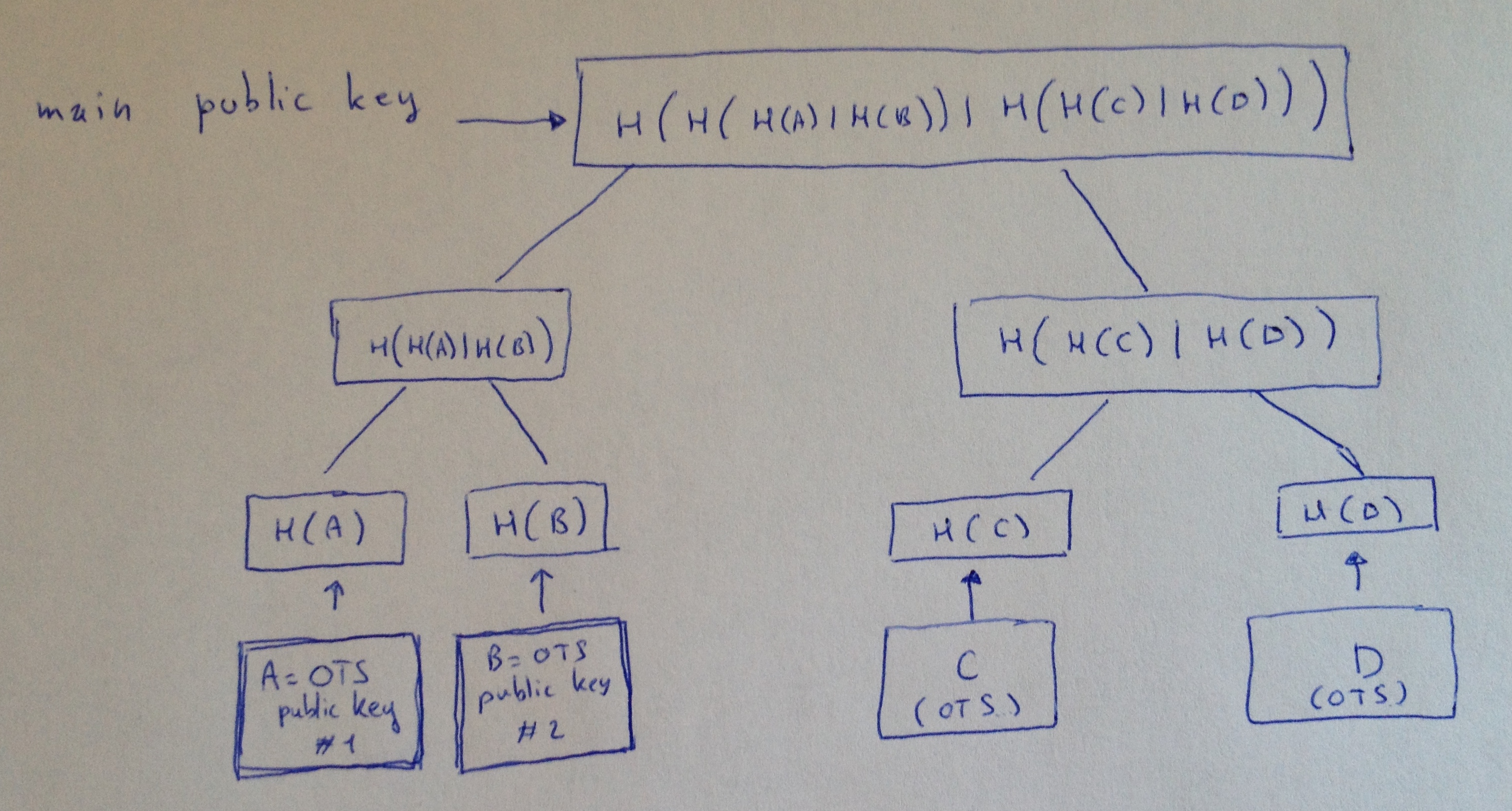
这样一来,当你要使用这棵树来签名的时候:第一次签名,你就使用第一个 OTS 公钥(即上图中的 “公钥 A”),并且绝不复用;第二次签名,就使用 “OTS 公钥 B”;然后是 “公钥C”,最后是 “公钥 D”。更大的默克尔树将允许你签名更多消息(而不需要更换公钥)。
这种想法吸引人的地方在于,你的公钥只是默克尔树的树根,每次你要签名的时候,你的签名都包含少量哈希值:认证路径。
在我们这个例子中,使用第一个 OTS 公钥(A)的签名将是:(1, 签名, 公钥 A, 认证路径)。其中:
- “1” 是用于签名的叶子的 索引号。记住:不能重复使用同一个叶子。所以,我们这种方案是一种带状态的方案(译者注:或者说,是需要记忆的方案)。
- “签名 ” 则是 OTS 公钥 A 背后的私钥(详见本系列的第一篇文章)。
- “公钥 ” 则是我们的 OTS 公钥,用于验证签名。
- “认证路径 ” 则是一系列的节点(也就是一组哈希值),让验证者可以重新计算出树根(我们的主公钥)(译者注:即验证签名公钥确实属于我们的主公钥)。
我们来看看认证路径。下图标出了在上述案例中,使用 OTS 公钥 A 签名之后,需要提供的认证路径:
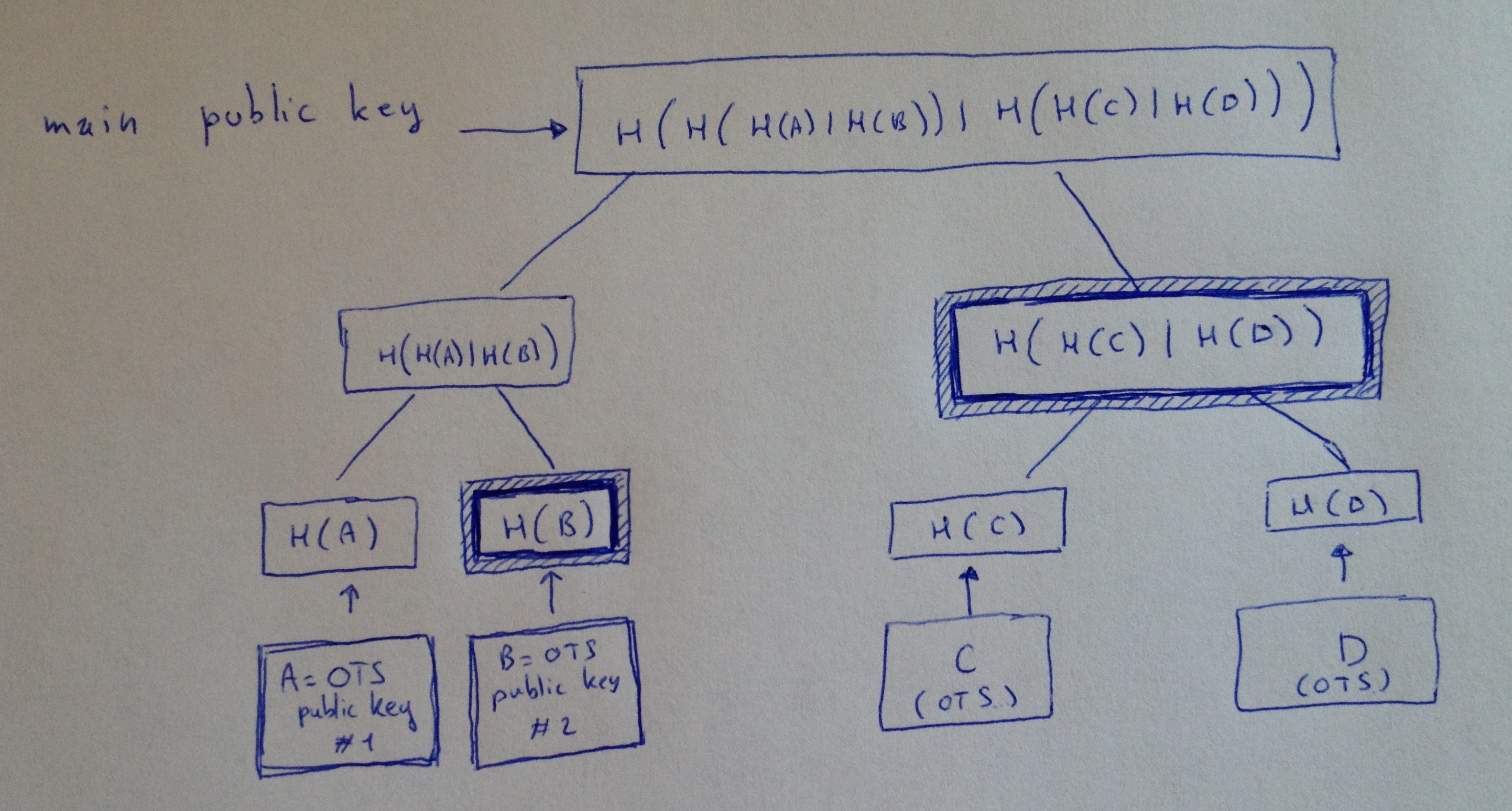
可以看出,有了我们的 OTS 公钥,以及两个哈希值(从签名叶子到树根的路径上的所有节点的相邻节点),我们就能计算出主公钥。因此,我们可以验证,它确实是一个来自主公钥的签名。
感谢这种技术,我们不需要所有的 OTS 公钥,就能验证主公钥。这样既节约空间,又节约计算量。
就是这样,这就是默克尔签名方案的简单概念。这是一种基于哈希函数的多次签名方案。